Project -- Gypsy Moth Dispersion in Massachusetts
[for project instructions,
click here]
OBJECT: The geographic dispersion of the Gypsy Moth, an insect pest threatening forests throughout North America, can be tracked and analysed using a Geographic Information System (GIS). The principle relies on the fact that diseased vegetation gives off different infra-red satellite image signatures than healthy vegetation. These signatures can be converted to pixel values, lending themselves to raster-based GIS analysis (rather than vector GIS).
30 years of satellite imagery is analysed to track the passage of this pest westward through the state of Massachusetts. The metric results of analysing raster images, using the IDRISI software, are used to develop a mathematical model (using linear regression) to predict the westward geographic spread of the Gypsy Moth in the Northeastern United States.
Highest pixel value is 9, but there
are 28 maps. Why is the highest value not 28? Because this
would imply that defoliation in a given pixel is going on for 28 years
in a row. However, there is probably a "post-defoliation" period
where, in fact, the leaves are all dead. Thus, a maximum value of
9 implies that defoliation only goes on in an area for a maximum of 9 years
(often less), after which there are no more leaves.
NOTE: macro is in c:\idrisiw\exercise\gypsy\masum.IML

Page 71, #1 -- Results of Extract
analysis:
Average years of defoliation, by
Forest Type
| Forest
Category |
Average
# of years |
Forest type
Description |
| 0 | 0.028032 | (unknown) |
| 7 | 0.494645 | Maple-beech-birch |
| 2 | 0.910714 | Spruce-fir |
| 1 | 1.058824 | White-red-jack Pine |
| 6 | 1.323077 | Elm-ash-cottonwood |
| 8 | 1.392246 | Nonforest |
| 5 | 1.916919 | Oak-hickory |
| 3 | 2.091324 | Loblolly-shortleaf Pine |
| 4 | 2.775862 | Oak-pine |
Observation: "Oak-pine" seems
most susceptible to defoliation by Gypsy Moth, while "Maple-beech-birch"
seems the least susceptible.
Page 72, #2 -- Other variables affecting susceptibility to defoliation:
Other factors might include forest
cover density, average rainfall, altitude. Testing of these other
factors would involve holding "forest type" constant (eg: test on "Oak-Pine"),
then correlating maps of cover density, rainfall, etc. with MASUMDEF.
High correlation coefficients would indicate a relationship, which itself
could be defined in a regression equation. Data needed would include
air photos, weather station readings, a Digital Elevation Model (DEM).
Page 73, #1 -- Resolution of the data set
The resolution of the data set is
at the county or district level. This will figure importantly
later in this exercise when we must determine the resolution at which we
will calculate the regression equation. Higher resolutions consume
more computer resources (eg: CPU time, RAM space used). By the way,
the "data resolution" itself, being integer, is 0 decimal places.
The spatial resolution is 6 kilometres per pixel (EG: 2256 km east-west
÷ 376 cols of pixels).
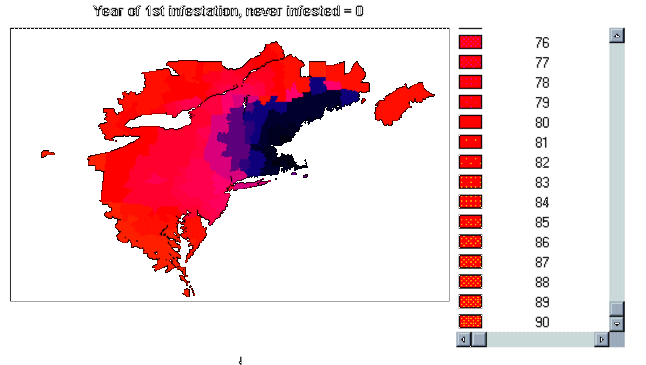
Page 73, #2 -- Year of infestation, value of pixels
The value of the Medford pixel is
"0", representing the year "1900", while the value of a pixel that has
never been infested (eg: in Atlantic Ocean) is "91", representing the year
"1991".
PROBLEM:
The resulting image, "YEARM", page
74, if created according to the instructions, is still incorrect.
Areas never infested, such as the ocean, and other land areas never infested,
are given the value "0". However, so is Medford, MA, the origin point
(year = 1900). Yet Medford is the most infested; giving Medford
the same pixel value as the ocean is misleading. Physically, on the
image "YEARM", it appears that the ocean shoreline has moved several kilometres
inland from Boston Harbour!
Page 74, #3 -- Decision on level of detail for regression (ie: "resolution")
This is a question of "weakest link
in the chain". When 2 or more images are being compared this way,
the final image should be at a resolution equivalent to the "coarsest"
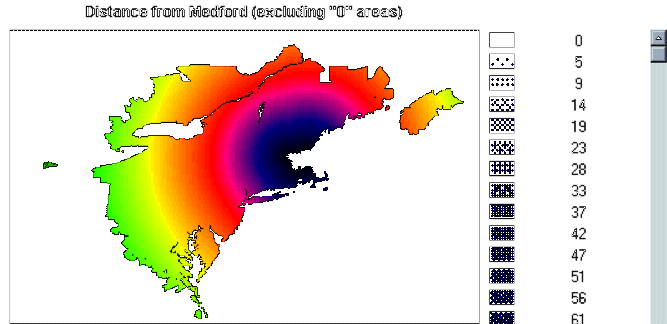
(ie: lowest) image. In the image "DISTM" the data can change from
pixel to pixel. However, in "YEARM" the data can only change from
county to county; within a given county, the data value is the same for
all pixels. This came about because "YEARM" was derived, through
several overlays, from "YEARSUM", which shows the sum of years of defoliation
at the county level and not at the pixel level.
Thus, values for each X,Y variable,
for the regression equation, should be taken at the county/district level,
since taking them at the pixel level would constitute a significant waste
of computer resources. The CPU, for instance, would be processing
data for several thousand pixels within a given county, where all the pixels
will ultimately have the same value anyway.
Page 75, #4 -- First line in values files for YEARM.VAL and DISTM.VAL
The first line in each file represents Medford, MASS. The "0" in the left column represents the location value of the county in which Medford is located, while the right column represents:
the distance from Medford (0 km, of course!), in the case of the DISTM.VAL data set, or
the year of infestation (year "00",
for "1900"), in the case of the YEARM.VAL data set.
NOTE: following are the results
of the regression analysis using all years (ie: 1900 to 1990, correlating
DISTM.VAL with YEARM.VAL) of data:
Distance (km) = 8.4843 x Year - 119.8549
R Squared 0.6458259
No. of Observations 430
Degrees of Freedom 428
Page 76, #5 -- Breaking regression analysis in 3 equations
The results of the regression analysis
using the years 1900 to 1915, correlating DISTM1.VAL with YEARM1.VAL are:
Distance (km) = 15.5236 x Year -
82.8037 (r= 0.6274; dof = 33)
The results of the regression analysis
using the years 1916 to 1965, correlating DISTM2.VAL with YEARM2.VAL are:
Distance (km) = 3.6418 x Year + 13.1478
(r= 0.6124; dof = 51)
The results of the regression analysis
using the years 1966 to 1990, correlating DISTM3.VAL with YEARM3.VAL are:
Distance (km) = 18.5008 x Year -
907.5202 (r= 0.7197; dof = 337)
The "X-coefficient", the value which
is multiplied against the "Year" independent variable, represents the rate
of diffusion. Thus, the diffusion rate was fastest during the most
recent period, the years 1966 to 1990, and slowest in the previous period,
the years 1916 to 1965.
Page 76, #6 -- Predicting the year of future infestations
This is simply an algebraic exercise.
Using the 3rd equation above (ie: years 1966 to 1990), we can
re-write it as:
Distance (km) + 907.5202 = 18.5008
x Year ........ or ...........
Year = (Distance + 907.5202 ) ÷
18.5008
For example, we can predict that
Chicago, approximately 1565 kilometres from Medford, MASS, will begin suffering
from Gypsy Moth infestation around the year 2033 (ie: 1565
+ 907.5202 = 2472.5202 ÷ 18.5008 = 133.64829 + "1900", since the
century part is dropped in the data sets, = 2033.6482).
Your comments on this assignment are welcome!